前一页
回目录
我国数学史上有一部堪与欧几里得《几何原本》媲美的书,这就是历来被尊为算经之首的《九章算术》。它是我国现存最早的数学专著,其传本包括《九章算术》本文、曹魏刘徽注、唐初李淳风等注释三部分内容。
《九章算术》集先秦至西汉我国数学知识之大成,其编纂也是集体劳动的成果。根据刘徽的记载,《九章算术》是从先秦“九数”发展来的。暴秦焚书,经术散坏。西汉张苍(?—前152年)、耿寿昌(前1世纪)收集遗文残稿,加以删补整理,编成《九章算术》。
《九章算术》包括了近百条一般性的抽象公式、解法,246个应用问题,分属方田、粟米、衰分、少广、商功、均输、盈不足、方程、勾股九章。
方田章提出了各种多边形、圆、弓形等的面积公式;分数的通分、约分和加减乘除四则运算的完整法则。后者比欧洲早1400多年。
粟米章提出比例算法,称为今有术;衰分章提出比例分配法则,称为衰分术;商功章除给出了各种立体体积公式外,还有工程分配方法;均输章用衰分术解决赋役的合理负担问题。今有术、衰分术及其应用方法,构成了包括今天正、反比例、比例分配、复比例、连锁比例在内的整套比例理论。西方直到15世纪末以后才形成类似的全套方法。
少广章介绍了开平方、开立方的方法,其程序与现今程序基本一致。这是世界上最早的多位数和分数开方法则。它奠定了我国在高次方程数值解法方面长期领先世界的基础。
盈不足章提出了盈不足、盈适足和不足适足、两盈和两不足三种类型的盈亏问题,以及若干可以通过两次假设化为盈不足问题的一般问题的解法。这也是处于世界领先地位的成果,传到西方后,影响极大。
方程章采用分离系数的方法表示线性方程组,相当于现在的矩阵;解线性方程组时使用的直除法,与矩阵的初等变换一致。这是世界上最早的完整的线性方程组的解法。在西方,直到17世纪才由莱布尼兹提出完整的线性方程的解法法则。这一章还引进和使用了负数,并提出了正负术——正负数的加减法则,与现今代数中法则完全相同;解线性方程组时实际还施行了正负数的乘除法。这是世界数学史上一项重大的成就,第一次突破了正数的范围,扩展了数系。外国则到7世纪印度的婆罗摩及多才认识负数。
勾股章提出了勾股数问题的通解公式:若a、b、c分别是勾股形的勾、股、弦,则
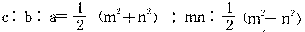
m>n。在西方,毕达哥拉斯、欧几里得等仅得到了这个公式的几种特殊情况,直到3世纪的丢番图才取得相近的结果,这已比《九章算术》晚约3个世纪了。勾股章还有些内容,在西方却还是近代的事。例如勾股章最后一题给出了这样一组公式:
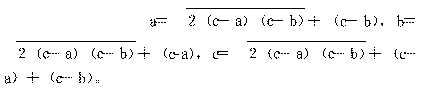
这在国外到19世纪末才由美国的数论学家迪克森得出。
《九章算术》确定了中国古代数学的框架,以计算为中心的特点,密切联系实际,以解决人们生产、生活中的数学问题为目的的风格。其影响之深,以致以后我国数学著作大体采取两种形式:或为之作注,或仿其体例著书;甚至西算传入中国之后,人们著书立说时还常常把包括西算在内的数学知识纳入“九章”的框架。
然而,《九章算术》亦有其不容忽视的缺点:没有任何数学概念的定义,也没有给出任何推导和证明。魏景元四年(263年),刘徽给《九章算术》作注,才大大弥补了这个缺陷。
刘徽是我国也是世界历史上最伟大的数学家之一。遗憾的是,他的生平我们现在知之甚少。据考证,他是山东邹平人。刘徽定义了若干数学概念,全面论证了《九章算术》的公式解法,提出了许多重要的思想、方法和命题,他在数学理论方面成绩斐然。
刘徽对数学概念的定义抽象而严谨。他揭示了概念的本质,基本符合现代逻辑学和数学对概念定义的要求。而且他使用概念时亦保持了其同一性。如他提出“凡数相与者谓之率”,把“率”定义为数量的相互关系。又如他把正负数定义为“今两算得失相反,要令正负以名之”,摆脱了正为余,负为欠的原始观念,从本质上揭示了正负数得失相反的相对关系。
《九章算术》的算法尽管抽象,但相互关系不明显,显得零乱。刘徽大大发展深化了中算中久已使用的率概念和齐同原理,把它们看作运算的纲纪。许多问题,只要找出其中的各种率关系,通过“乘以散之,约以聚之,齐同以通之”,都可以归结为今有术求解。
一平面(或立体)图形经过平移或旋转,其面积(或体积)不变。把一个平面(或立体)图形分解成若干部分,各部分面积(或体积)之和与原图形面积(或体积)相等。基于这两条不言自明的前提的出入相补原理,是我国古代数学进行几何推演和证明时最常用的原理。刘徽发展了出入相补原理,成功地证明了许多面积、体积以及可以化为面积、体积问题的勾股、开方的公式和算法的正确性。
在数学证明中成功地运用无穷小分割和极限思想,是刘徽最杰出的贡献。
《九章算术》提出圆面积公式S=l/2·r(S为圆面积,l为圆周长,r为半径)。为证明这个公式,刘徽从圆内接正六边形S6(称为六觚)开始割圆,依次得圆内接正十二边形S12,圆内接正二十四边形S24,……S6·2的n次方……所有S6·2的n次方<S,但“割之弥细,所失弥少。割之又割,以至于不可割,则与圆周合体而无所失矣。”这相当于:
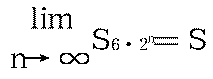
然后他证明
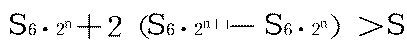
而
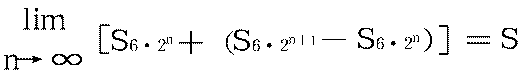
。于是刘徽就把圆化为与之合体的内接正多边形来求面积,再把这个正多边形分割成以每边为底以圆心为顶点的无穷多个小三角形之和,所谓“觚而裁之,每辄自倍。
故以半周乘半径而为圆幂”。从明证明了S=l/2·r。刘批评了以往“圆径一而周三”的错误,指出此公式中周径是“至然之数”,即圆周率π。他以此公式为基础,求出了π的两个近似值157/20和3927/1250,在中国首次创立了求圆周率的科学方法,奠定了我国圆周率研究在世界长期领先的基础。
刘徽注关于体积问题的论述已经接触到现代体积理论的核心问题,指出四面体体积的解决是多面体体积理论的关键,而用有限分割和棋验法无法解决其体积。为了解决这个问题,他提出了一个重要原理“邪解壍堵,其一为阳马,一为鳖臑。
阳马居二,鳖臑居一,不易之率也”,今称为刘徽原理。刘徽平分壍堵的长、宽、高,通过出入相补,可以证明在壍堵的3/4中上述原理成立;而剩余的1/4与原壍堵的结构相同,可以重复上述分割,又可以证明其3/4中这个原理成立。这个过程可以无限继续下去,“半之弥少,其余弥细。至细曰微,微则无形。由是言之,安取余哉?”完成了该原理的证明。由壍堵的体积公式v=1/2abh,便证明《九章算术》提出的阳马体积公式v=1/3abh,鳖臑的体积公式v=1/6abh。近代数学大师高斯、希尔伯特才讨论这个问题,已是近100多年以来的事。
刘徽注多方面表述了今天称之为祖暅之原理的命题,并由此证明了《九章算术》中球体积公式的错误。他设计了牟合方盖,指出球与牟合方盖的体积之比是π∶4,只要求出后者的体积就可以求出球体积了。他尽管没能求出牟合方盖的体积,但诚恳地表示“以俟能言者”,表现出一位伟大学者的坦荡胸怀。这个问题后来由祖冲之父子彻底解决,李淳风注释《九章算术》时详细记述了祖氏的方法。
刘徽注中还有不少有价值的成就。如对开方不尽,提出继续开方,求其“微数”,以十进分数逼近无理根,开十进小数之先河;他还认识到不定方程有无穷多组解,等等。刘徽注形成了一套数学体系,他说“事类相推,各有攸归,故枝条虽分而同本干知,发其一端而已。”把数学看作一株枝条虽然分开但本干相同的大树。他认为数学是“规矩”与“度量”亦即空间形式与数量关系的统一。基于这些深刻的认识,他的证明除个别失误外,都论点明确,论据充分,条理清晰,推理严谨;而且大都使用演绎推理,没有循环论证。是严格的数学证明。有了刘徽的证明。《九章算术》的公式解法,才建立在真实可靠的基础上。
《九章算术》及其刘徽注,以杰出的数学成就,独特的数学体系。不仅对东方数学,而且对整个世界数学的发展产生了深远的影响,在科学史上占有极为重要的地位。它的出现,标志着从公元前1世纪开始,中国取代古希腊成为世界数学的中心,为此后中国数学领先世界1500多年奠定了基础。今天,随着计算机的出现和发展,它所蕴含的算法和程序化思想,仍给数学家以启迪。吴文俊先生指出“《九章》所蕴含的思想影响,必将日益显著,在下一世纪中凌驾于《原本》思想体系之上,不仅不无可能,甚至说是殆成定局,本人认为也绝非过甚妄测之辞。”
------------------
一鸣扫描,雪儿校对
前一页
回目录